기록
역전파 - BackPropagation 본문
입력 데이터를 신경망 네트워크 모델에 인가하여 얻은 예측값(Pred)과 실제값(Label)의 오차(Error)를 최소화 하기 위해 역전파(BackPropagation)과정에서 가중치(Weight)인 파라미터를 업데이트 하는 과정을 계산하여 이해 하려고 한다.
설명을 위한 신경망 구조
신경망 네트워크는 입력층, 은닉층, 출력층으로 구성되어 있다. 설명을 보다 쉽게 이해하기 위해서 2개의 입력, 활성화 함수 시그모이드, 2개의 출력을 사용한다.

순전파(Forward Propagation)
위의 입력값을 활용하여 순전파를 통해 얻는 예측값을 구해 본다.

각 입력과 가중치의 곱의 합으로 z1,z2를 구한다. 다음으로 h(x)인 시그모이드 활성화 함수를 지난다.

시그모이드 수식에 위에서 구한 z1,z2 값을 넣어 h1,h2를 구한다.
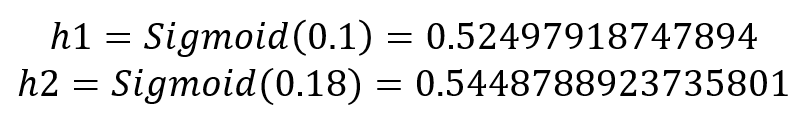
활성함수를 거쳐 나온 값에 가중치 곱의 합으로 은닉층의 출력 z3,z4를 구한다.
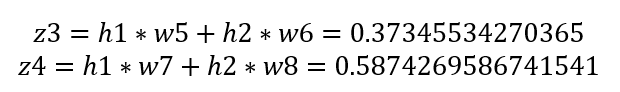
마지막으로 은닉층의 출력에 활성화 함수를 거쳐 출력값 o1,o2를 구한다.
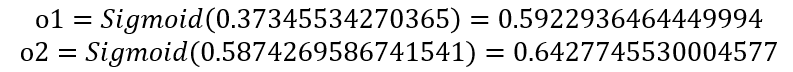
입력 데이터에 대한 예측값 o1,o2를 구하였다. 다음으로는 예측한 값과 실제값간의 오차(Error)를 구하기 위해서 손실 함수로 Mean Square Error(MSE)를 사용한다.

역전파(Back Propagation)
다음으로는 가중치를 업데이트하기 위해서 역전파를 수행한다.
순전파의 방향과 반대로 진행을 해야하기에 먼저 w5,w6,w7,w8 가중치를 업데이트 한다.
가중치를 업데이트를 위해서 편미분을 사용한다.
편미분은 변수가 2개 이상인 함수에서 변수 1개의 변화에 따른 기울기(변화률)을 알고 싶을 때 사용한다.
즉, 가중치의 변화에 따른 에러의 변화률을 알기 위해 사용한다.
(∂E_total)/∂w5를 계산하기 위해 미분의 연쇄 법칙(Chain rule)를 사용한다.
연쇄 법칙은 변수가 여러 개일 때, 어떤 변수에 대한 다른 변수의 변화율을 알아낼때 사용한다.

각 항을 분석하면 다음과 같다.

가장 오른쪽 항의 Target_o2와 Output_o2는 상수 취급이 되어 사라진다. 결론적으로 왼쪽항을 보면된다.

왼쪽항은 합성함수의 미분법을 사용하여 구한다.


위의 식들을 통해 w5를 업데이트 하기 위한 첫번째 항을 구하였다.
다음은 두번째 항을 구한다.
o1은 Sigmoid(z3)과 같다.
두번째 항의 o1의 결과는 Sigmoid를 통해서 얻은 결과이기에 Sigmoid를 미분하면 Sigmoid(x) * (1-Sigmoid(x))를 얻을 수 있다.

마지막 세번째 항은 h1과 동일하다.
z3 = h1 * w5 + h2 * w6 에서 h1만 남게 된다.

결론적으로 모든항을 곱하였을때 0.0243776352560694 를 얻는다.
다음으로는 경사 하강법을 통해 가중치 w5를 업데이트하는데 공식은 아래와 같다.
학습률(learning rate)인 α는 0.001 이라고 설정.

이를 통해서 w5 가중치의 값을 0.4 에서 0.3999756223647439로 업데이트 한다.
위와 같은 방식으로 w5,w6,w7,w8 을 업데이트하고 다시 w1,w2,w3,w4를 업데이트 적용한다.
그리고 다시 forward propagation을 통해서 업데이트된 가중치를 활용해 예측값을 구하고 Error를 기반으로 또 가중치 업데이트.. 와 같은 반복적인 수행을 통해서 신경망 네트워크의 Error가 최대한 근사하도록 학습한다.
'딥러닝' 카테고리의 다른 글
| RNN 과 LSTM 정리 (0) | 2023.06.22 |
|---|---|
| 딥러닝(Deep Learning) 용어 - 배치 사이즈(Batch Size), 이터레이션(Iteration), 에포크(Epoch) (0) | 2021.07.21 |
| 딥러닝(deep learning) 용어 - 파라미터와 하이퍼파라미터 (0) | 2021.07.21 |
| 데이터 라벨링 (0) | 2021.06.19 |
| xml 파일 데이터를 활용하여 Image에 box 그리기 (0) | 2021.06.16 |

